Table of Contents
Tabletap
- 3 (oder mehr) Kontaktmikrophone (Piezo) werden auf einem Tisch montiert. Damit soll gemessen werden, wann ein Finger den auf den Tisch tippt. Aus den Laufzeitdifferenzen des Schalls soll die Position bestimmt werden.
- Dazu braucht es erst einmal eine gute Verstärkerschaltung. Erste gute Ergebnisse wurden mit folgender Schaltung erhalten: http://davidhoulding.blogspot.com/2014/02/high-sensitivity-vibration-sensor-using.html
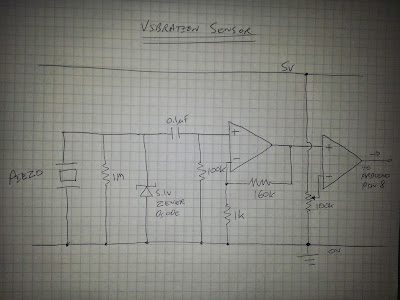
- Video vom Test der Schaltung: https://t.co/bWnQNcHFeu
- Um die Laufzeiten möglichst genau zu messen, verwenden wir Interrupts auf dem ESP32. Ein POC findet sich hier: https://github.com/techlabksbg/tabletap
Mathematik dahinter
Der Zeitpunkt, zu dem der Tisch berührt wurde ist nicht bekannt. Es somit nur die Laufzeitdifferenzen zu den einzelnen Mikrophonen bekannt. Kennt man nur zwei Mikrophone (und die Schallgeschwindigkeit), liegt der Berührungspunkt auf einem Hyperbelast.
Es sind also Hyperbeln in allgemeiner Lage zu schneiden, was zu potenziell 4 Schnittpunkten führen kann, also Gleichungen 4. Grades.
Input
Gegeben:
- Positionen $F_1$, $F_2$, $F_3$ als $(x,y)$-Koordinaten
- Zeitstempel $t_1$, $t_2$, $t_3$ wann das Signal angekommen ist.
Gesucht:
- Position $P$, wo die Berührung stattgefunden hat. Oder $t_0$, wann die Berührung stattgefunden hat.
Annahmen:
- $t_1 < t_2$ und $t_1 < t_3$. D.h. $F_1$ hat als erstes die Berührung registriert.
- Schallgeschwindigkeit $v$ bekannt. Es kann also direkt mit den Abstandsdifferenzen gearbeitet werden:
- $\overline{PF_2}-\overline{PF_1} = d_2 = \frac{t_2-t_t}{v}$ und $\overline{PF_3}-\overline{PF_1}=d_3$.
Ansätze:
- Schnitt zweier Hyperbeläste in «allgemeiner» Lage, wobei jeweils ein Brennpunkt gemeinsam ist. In GeoGebra sieht es so aus, als gäbe es für spitzwinklige Dreiecke $F_1F_2F_3$ nur genau eine Lösung, für stumpfwinkle aber 2.
- Affine Transformation einer Hyperbel auf die Form $y=\frac{1}{x}$, die andere in allgemeiner Form schreiben, einsetzen, Polynom 4. Grades lösen (z.B. mit Newton-Verfahren).
- $P$ schätzen, iterativ verbessern (funktioniert ungefähr, Konvergenz ist langsam, speziell wenn $P$ nahe ein einem $F_i$ liegt.
- Abstände in Funktion von $t_0$ schreiben, nummerisch auflösen.
$r = \overline{PF_1}$ bestimmen
Sei $s=\overline{F_1F_2}$.
Sei $\vec{f_x} = \frac{1}{s}\vec{F_1F_2}$ und $\vec{f_y}$ der um $+90^\circ$ gedrehte $\vec{f_x}$.
Sei nun $\vec{OP} = \vec{OF_1} + a\vec{f_x} + h\vec{f_y}$. Dann gilt: $$r^2-a^2=\left(r+d_{2}\right)^2-\left(s-a\right)^2$$
Daraus folgt $$a={{s^2-2\,d_{2}\,r-d_{2}^2}\over{2\,s}}$$ und $$ h^2 = r^2-a^2 = r^2-{{\left(s^2-2\,d_{2}\,r-d_{2}^2\right)^2}\over{4\,s^2}} = -{{s^2}\over{4}}-{{d_{2}^2\,r^2}\over{s^2}}-{{d_{2}^3\,r}\over{s^2 }}-{{d_{2}^4}\over{4\,s^2}}+r^2+d_{2}\,r+{{d_{2}^2}\over{2}} $$ Das ist Polynom 2.Grades in $r$ mit den Koeffizienten (aufsteigende Potenzen von $r$):
[-((s-d_2)^2*(s+d_2)^2)/(4*s^2),(d_2*(s-d_2)*(s+d_2))/s^2,((s-d_2)*(s+d_2))/s^2]
Seien $(x,y)$ die Koordinaten von $F_3$ im System $(F_1, \vec{f_x}, \vec{f_y})$.
Es gitl $\overline{PF_3} = r+d_3$:
$$\left(y-\sqrt{r^2-{{\left(s^2-2\,d_{2}\,r-d_{2}^2\right)^2}\over{4 \,s^2}}}\right)^2+\left(x-{\it as}\right)^2=r+d_{3} $$
$$y^2-2\,\sqrt{-{{s^2}\over{4}}-{{d_{2}^2\,r^2}\over{s^2}}-{{d_{2}^3 \,r}\over{s^2}}-{{d_{2}^4}\over{4\,s^2}}+r^2+d_{2}\,r+{{d_{2}^2 }\over{2}}}\,y+x^2-2\,{\it as}\,x-{{s^2}\over{4}}-{{d_{2}^2\,r^2 }\over{s^2}}-{{d_{2}^3\,r}\over{s^2}}-{{d_{2}^4}\over{4\,s^2}}+r^2+ d_{2}\,r-r-d_{3}+{{d_{2}^2}\over{2}}+{\it as}^2=0$$
Wurzel isolieren, quadrieren, alles auf eine Seite, mit $16s^4$ erweitert liefert folgendes Polynom vierten Grades in $r$:
eq: r^2-a^2 = (r+d_2)^2-(s-a)^2; ar:rhs(solve(eq, a)[1]); h2: r^2-ar^2; string(create_list(factor(coeff(expand(h2),r,i)),i,0,2)); eq2: (x-ar)^2+(y-sqrt(h2))^2 = r+d_3; expand(eq2)-rhs(eq2); string(expand(eq2)-rhs(eq2)); eq3:expand(eq2)-rhs(eq2); string(eq3); eq4:eq3+2*sqrt((-s^2/4)-(d_2^2*r^2)/s^2-(d_2^3*r)/s^2-d_2^4/(4*s^2)+r^2+d_2\ *r+d_2^2/2)*y; eq5: expand(lhs(eq4)^2) = expand(rhs(eq4)^2); eq6: eq5-rhs(eq5); create_list(factor(coeff(lhs(eq6),r,i))*s^4*16,i,0,4);
Weiter buddeln
$$h^2 = -{{\left(s-d_{2}\right)\,\left(s+d_{2}\right)\,\left(s-2\,r-d_{2} \right)\,\left(s+2\,r+d_{2}\right)}\over{4\,s^2}}$$
Die Gleichung erst mal $h$ geschrieben:
$$\left(y-h\right)^2+\left(x-a\right)^2=r+d_{3}$$
$h$ isoliert:
$$y^2+x^2-2\,a\,x-r+h^2-d_{3}+a^2=2\,h\,y$$
quadriert:
$$\left(y^2+x^2-2\,a\,x-r+h^2-d_{3}+a^2\right)^2=4\,h^2\,y^2$$
Alles nach links, Faktorisieren, Freude haben (und dann wieder nicht, weil wieder $h$ drin vorkommt):
$$\left(y^2-2\,h\,y+x^2-2\,a\,x-r+h^2-d_{3}+a^2\right)\,\left(y^2+2\, h\,y+x^2-2\,a\,x-r+h^2-d_{3}+a^2\right)=0$$
Man kommt schlussendlich wieder auf das gleiche Polynom wie vorher:
[(s^2*y^4+2*s^2*x^2*y^2-2*s^3*x*y^2+2*d_2^2*s*x*y^2+s^4*y^2-2*d_3*s^2*\ y^2-2*d_2^2*s^2*y^2+d_2^4*y^2+s^2*x^4-2*s^3*x^3+2*d_2^2*s*x^3+s^4*x^2-2*d_3*s^\ 2*x^2-2*d_2^2*s^2*x^2+d_2^4*x^2+2*d_3*s^3*x-2*d_2^2*d_3*s*x+d_3^2*s^2)/s^2,(2*\ (2*d_2*s*x*y^2-2*d_2*s^2*y^2-s^2*y^2+2*d_2^3*y^2+2*d_2*s*x^3-2*d_2*s^2*x^2-s^2\ *x^2+2*d_2^3*x^2+s^3*x-2*d_2*d_3*s*x-d_2^2*s*x+d_3*s^2))/s^2,-(2*s^2*y^2-4*d_2\ ^2*y^2-2*s^2*x^2-4*d_2^2*x^2+2*s^3*x-2*d_2^2*s*x+4*d_2*s*x+2*d_3*s^2-s^2)/s^2,\ (2*(2*d_2*x-s))/s,1]
eq10: (x-a)^2+(y-h)^2=r+d_3; eq11:expand(eq10)-rhs(eq10)+2*h*y; eq12:eq11^2; h2: factor(expand(r^2 - ar^2)); eq13:expand(eq12-rhs(eq12)), h^2=h2; string(%); eq14: eq13, a=ar; eq15:factor(eq14*s^2); create_list(factor(coeff(expand(lhs(eq14)),r,i)),i,0,4);